Componentes de uma Série Temporal
Autor: SergioJr
Data: 08 de Agosto de 2023
Categorias: Ciência de Dados

Os principais componentes de uma Série Temporal
São eles: Tendência, Sazonalidade e Aleatoriedade. Abordaremos sobre cada um deles, falaremos de como detecta-los e sobre sua importância no contexto da Ciência de Dados.
O que é Tendência?
Se for pra responder rapidamente, tendência capta elementos de longo prazo relacionados com a série de tempo, porém vamos explorar melhor isso.
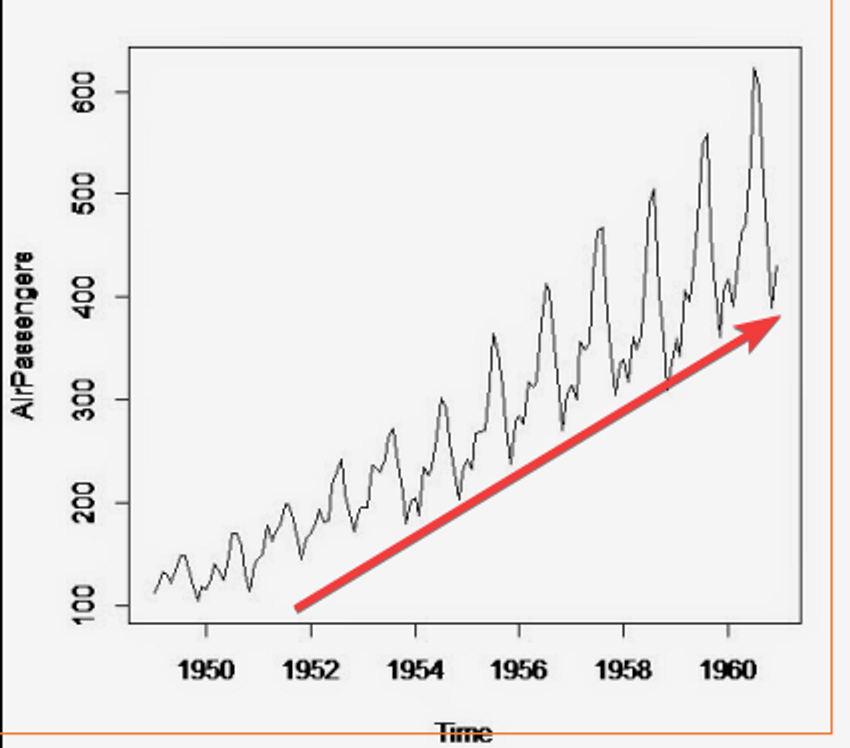
Assim como nome sugere, esse componente é uma tendência em relação aos dados da série. Se observarmos o gráfico ao lado podemos ver que existe uma tendência, a de crescimento. O modelo mais comum de tendência assim como na regressão, é o linear.
A tendência pode ser ascendente, descendente ou relativamente plana, dependendo da natureza dos dados. A identificação da tendência é crucial para entender se os dados estão apresentando um crescimento, declínio ou estabilidade ao longo do tempo.
Como detectar uma Tendência?
Existem várias abordagens diferentes para identificar a tendência em uma série temporal:
Médias Móveis: Este método envolve o cálculo de médias de um número fixo de pontos de dados consecutivos para suavizar flutuações e destacar a tendência subjacente.
Regressão Linear: A regressão linear é usada para modelar uma linha reta que melhor se ajusta aos dados, permitindo quantificar a direção e magnitude da tendência.
Decomposição de Séries Temporais: A série temporal pode ser decomposta em componentes, incluindo tendência, sazonalidade e resíduos, usando métodos como decomposição clássica ou decomposição baseada em filtragem (falaremos sobre decomposição de uma série temporal ainda neste artigo).
Métodos Estatísticos e Modelos Avançados: Algoritmos mais complexos, como ARIMA (Médias Móveis Integradas com AutoRegressão) e modelos de suavização exponencial, podem ser usados para modelar tendências mais complexas e sazonalidades.
Qual o papel da Tendência na Ciência de dados?
O componente de tendência é crucial na análise de séries temporais e tem um papel significativo na Ciência de Dados, pois com ela é possível fazer:
Previsão: Uma vez que a tendência é identificada e modelada, é possível fazer previsões sobre os valores futuros da série temporal. Isso é valioso para tomar decisões informadas.
Tomada de Decisões: A análise da tendência em dados pode ajudar as empresas a tomar decisões estratégicas, como planejamento de recursos, investimentos e alocação de recursos.
Detecção de Anomalias: A tendência também pode ser usada para detectar anomalias ou mudanças significativas nos padrões de dados, o que pode indicar problemas ou oportunidades.
Monitoramento de Desempenho: A análise de tendências ajuda a monitorar o desempenho ao longo do tempo e a avaliar o sucesso de ações ou estratégias implementadas.
Em resumo, o componente “Tendência” em uma série temporal descreve a direção geral dos dados ao longo do tempo e é uma parte essencial da análise de séries temporais na Ciência de Dados. Ele fornece insights valiosos para previsões, tomada de decisões e monitoramento de desempenho.
O que é Sazonalidade?
Efeito de um elemento que ocorre em intervalos de tempo regulares, no mesmo gráfico, podemos ver o transporte de passageiros, é natural que exista uma maior frequência de passageiros em período de férias, e em todos os anos existem picos:
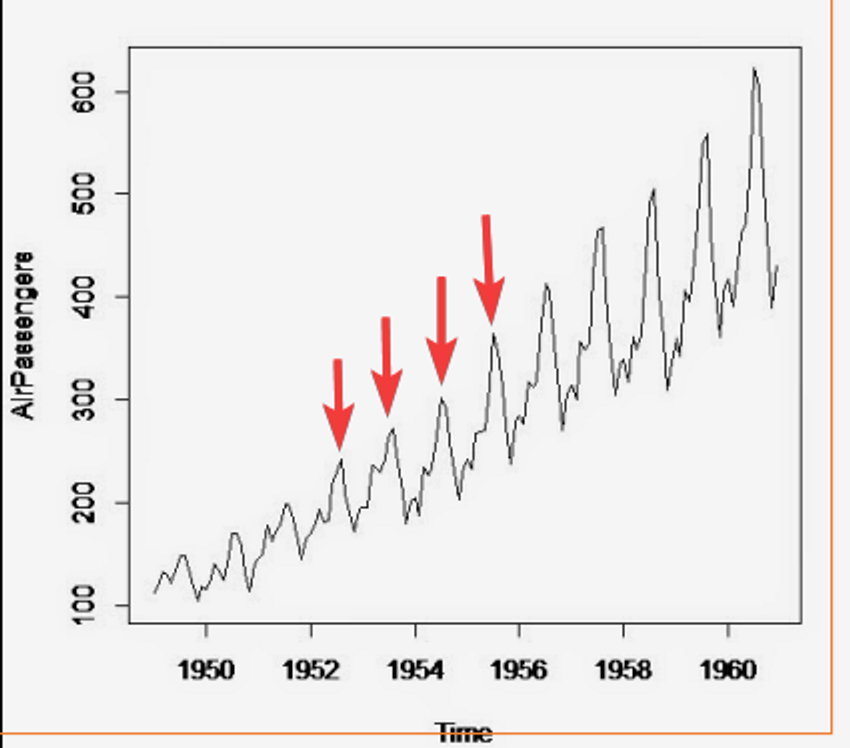
Esses padrões geralmente estão associados a fatores sazonais, como estações do ano, feriados, eventos culturais ou ciclos de negócios. A sazonalidade implica que há flutuações regulares nos dados que ocorrem em momentos específicos.
Como detectar a Sazonalidade?
Análise Visual: Um gráfico da série temporal ao longo do tempo pode revelar padrões sazonais, como oscilações regulares.
Autocorrelação: A análise de autocorrelação pode ajudar a identificar padrões de repetição nos dados que podem ser atribuídos à sazonalidade.
Decomposição de Séries Temporais: A decomposição separa a série temporal em componentes, incluindo tendência, sazonalidade e resíduos, permitindo a análise mais aprofundada da sazonalidade.
Análise de Frequência: A transformação de Fourier pode ser aplicada para analisar as frequências presentes nos dados e identificar os componentes sazonais.
Qual o papel da Sazonalidade na Ciência de dados?
Previsões Mais Precisas: A identificação e modelagem da sazonalidade permitem fazer previsões mais precisas, levando em consideração os padrões recorrentes que afetam os dados.
Planejamento Estratégico: A sazonalidade é essencial para setores como varejo e turismo, onde as empresas precisam ajustar suas estratégias com base em períodos de alta demanda sazonal.
Otimização de Recursos: Compreender os padrões sazonais ajuda a otimizar o uso de recursos, como estoque, pessoal e capacidade de produção.
Análise de Desempenho: A análise da sazonalidade pode revelar informações sobre o desempenho ao longo do ano e ajudar na avaliação de campanhas sazonais ou promoções.
Detecção de Anomalias Sazonais: Padrões sazonais irregulares podem indicar anomalias, que podem ser importantes para identificar problemas ou oportunidades inesperadas.
O que é Aleatoriedade?
O componente de aleatoriedade, também conhecido como “ruído” ou “erro”, em uma série temporal refere-se às variações imprevisíveis e não sistemáticas que não podem ser atribuídas à tendência ou à sazonalidade. Essas variações podem ser causadas por fatores aleatórios, flutuações econômicas, eventos imprevisíveis ou erros de medição. O componente de aleatoriedade representa a incerteza inerente aos dados e é uma parte natural de qualquer série temporal.
Qual sua importância?
Modelagem Estatística: A presença de aleatoriedade torna a modelagem estatística mais desafiadora, mas também mais realista. Modelos estatísticos podem ajudar a separar os componentes de tendência, sazonalidade e aleatoriedade para entender melhor os dados.
Avaliação de Modelos: A presença de aleatoriedade permite avaliar a eficácia dos modelos de previsão, uma vez que a capacidade de um modelo de prever essas flutuações imprevisíveis é um indicador de sua robustez.
Tomada de Decisões: Compreender a aleatoriedade ajuda a tomar decisões mais informadas, reconhecendo que nem todas as variações nos dados são previsíveis ou controláveis.
Análise de Incertezas: A ciência de dados frequentemente lida com incertezas nos dados. O componente de aleatoriedade é um exemplo de incerteza que deve ser considerada ao tomar decisões com base em análises de dados.
Como trata-la
Embora a aleatoriedade não possa ser completamente eliminada, ela pode ser modelada e tratada:
Modelos Estatísticos: Métodos como ARIMA (Médias Móveis Integradas com AutoRegressão) e modelos de suavização exponencial levam em conta o componente de aleatoriedade ao modelar tendências e sazonalidades.
Simulações: Simulações estatísticas podem ajudar a entender a faixa de possíveis resultados devido à aleatoriedade, auxiliando na tomada de decisões sob incerteza.
Análise de Resíduos: A análise de resíduos (diferença entre os valores reais e os previstos) ajuda a identificar padrões no componente de aleatoriedade e verificar a qualidade dos modelos.
Decomposição
É uma parte importante dos estudos das séries temporais, aqui, pegamos os elementos ou componentes o qual vimos acima e separamos eles, e assim podemos ter uma compreensão melhor da série temporal. Abaixo temos a mesma série temporal que vimos acima (dos passageiros):
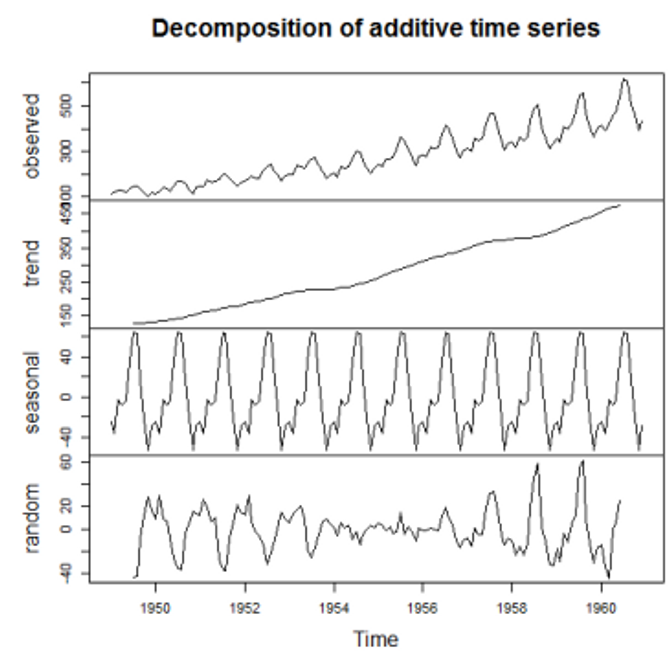
No primeiro retângulo temos a série temporal original (com todos componentes juntos). Abaixo dele temos o elemento tendência, veja que se extraiu o elemento tendência dos dados observados (série original do primeiro retângulo), vemos que ela foi extraída sem o elemento sazonal, temos apenas a tendência de crescimento. Abaixo dele no terceiro retângulo temos o elemento sazonal, podemos ver como ele fica mais claro e melhor observável quando extraímos ele, podemos ver que ele tem uma grande regularidade onde todos os picos são praticamente iguais. E por fim temos o elemento aleatório, basicamente é o que sobrou, os elementos inexplicáveis matematicamente.
Por que devemos decompor nossas Séries Temporais?
Entendimento dos Padrões: A decomposição ajuda a entender e interpretar os diferentes padrões presentes nos dados, facilitando a análise e a tomada de decisões.
Previsões Precisas: Uma vez que os componentes foram identificados, é possível fazer previsões mais precisas, considerando tendências, sazonalidades e ciclos.
Avaliação de Modelos: A decomposição pode ajudar a avaliar a qualidade dos modelos de previsão, identificando se os modelos estão capturando adequadamente os diferentes componentes.
Detecção de Anomalias: A análise dos resíduos (parte não explicada pela decomposição) pode ajudar a identificar anomalias ou eventos excepcionais.
Tomada de Decisões: Compreender a decomposição dos dados auxilia na tomada de decisões mais informadas e estratégicas.
Bonûs: Previsões
Quando falamos em previsão em séries temporais, diferente da regressão linear, nós estamos falando sempre em extrapolar, olhar os dados para frente, e a previsão só é possível com uma maior precisão quando a série temporal tem elementos que possam ser explicados matematicamente. Existem várias técnicas de previsão, clássicas como a do ARIMA (a qual falamos em meu primeiro artigo), suavização exponencial e redes neurais artificiais especificamente as recorrentes, principalmente a LSTM. Abaixo temos uma previsão feita com ARIMA:
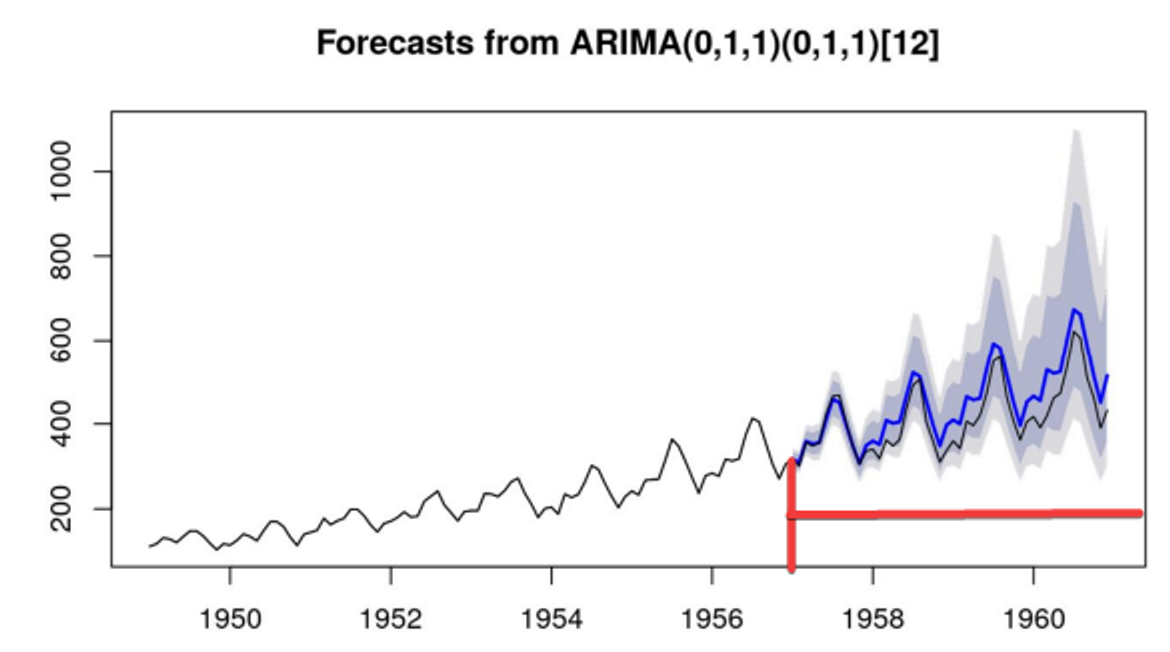
Assim como qualquer outra previsão, até a linha vermelha temos nossos dados e pra frente nossa previsão. Quanto mais pra frente você prever, deve-se esperar uma variação maior, e é exatamente isso que as áreas em cinza mostram:
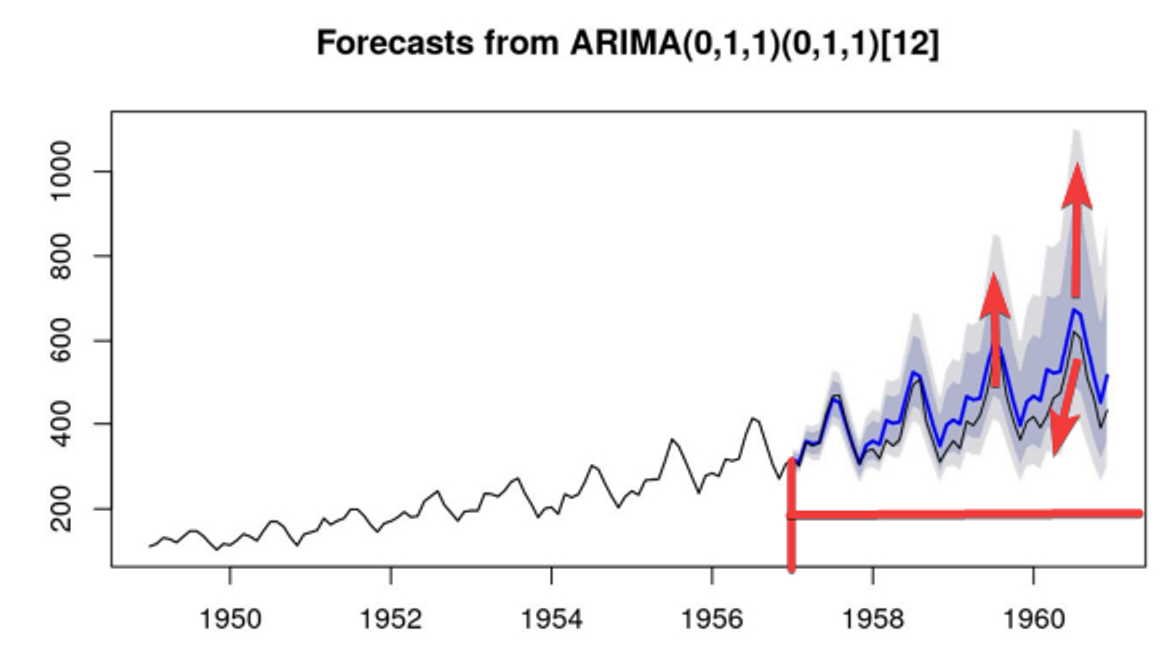
E isso é um processo normal. Existem outras técnicas para previsão de séries temporais como a suavização exponencial a qual dá pesos aos dados, os dados mais perto da nossa previsão terão um peso maior, influenciarão e contribuirão mais com a nossa previsão, os dados mais longe irão contribuir menos:
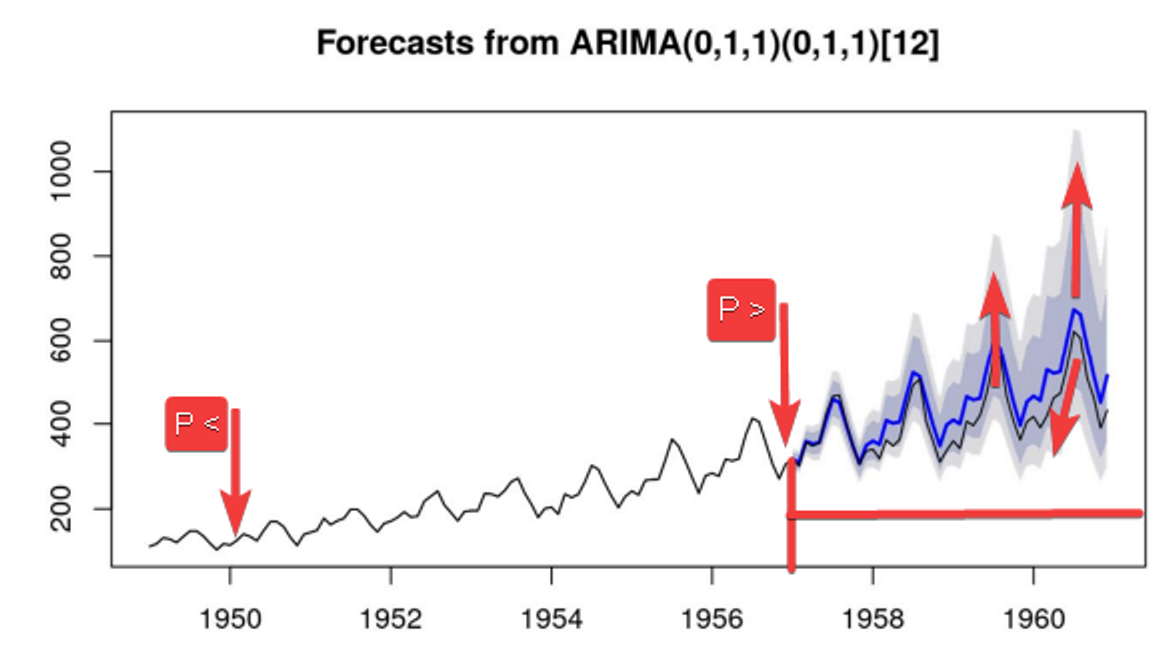
É natural que as coisas e o mundo mude, logo é intuitivo que os acontecimentos mais recentes influenciem mais em nossa previsão.
Conclusão
À medida que concluímos esta jornada explorando as Séries Temporais, espero que tenha ficado claro o impacto significativo que elas podem ter em todo e qualquer setor.
Obrigado por se juntar a mim nesta discussão. Sua contribuição é inestimável e juntos podemos espalhar o conhecimento da Ciência de dados e tecnologia para cada vez mais pessoas. Obrigado por ler até aqui!
Obrigado por me acompanhar nesta viagem!
Que tal começarmos outra?
🚀